Total quotient ring
In abstract algebra, the total quotient ring,[1] or total ring of fractions,[2] is a construction that generalizes the notion of the field of fractions of a domain to commutative rings that may have zero divisors. The construction embeds the ring in a larger ring, giving every non-zerodivisor of the smaller ring an inverse in the larger ring. Nothing more in the small ring can be given an inverse, because zero divisors are impossible to invert[3]. In light of this, the total ring of quotients is optimal in the sense that "everything that could have an inverse gets an inverse".
Contents |
Definition
Let  be a commutative ring and let
be a commutative ring and let  be the set of elements which are not zero divisors in
be the set of elements which are not zero divisors in  ; then
; then  is a multiplicatively closed set that does not contain zero. Hence we may localize the ring
is a multiplicatively closed set that does not contain zero. Hence we may localize the ring  at the set
at the set  to obtain the total quotient ring
to obtain the total quotient ring 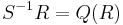 .
.
If  is a domain, then
is a domain, then 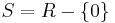 and the total quotient ring is the same as the field of fractions. This justifies the notation
and the total quotient ring is the same as the field of fractions. This justifies the notation 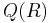 , which is sometimes used for the field of fractions as well, since there is no ambiguity in the case of a domain.
, which is sometimes used for the field of fractions as well, since there is no ambiguity in the case of a domain.
Since  in the construction contains no zero divisors, the natural map
in the construction contains no zero divisors, the natural map 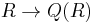 is injective, so the total quotient ring is an extension of
is injective, so the total quotient ring is an extension of  .
.
Examples
The total quotient ring 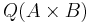 of a product ring is the product of total quotient rings
of a product ring is the product of total quotient rings  . In particular, if A and B are integral domains, it is the product of quotient fields.
. In particular, if A and B are integral domains, it is the product of quotient fields.
The total quotient ring of the ring of holomorphic functions on an open set D of complex numbers is the ring of meromorphic functions on D, even if D is not connected.
In an Artinian ring, all elements are units or zero divisors. Hence the set of non-zero divisors is the group of units of the ring, 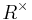 , and so
, and so 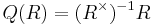 . But since all these elements already have inverses,
. But since all these elements already have inverses, 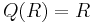 .
.
The same thing happens in a commutative von Neumann regular ring R. Suppose a in R is not a zero divisor. Then in a von Neumann regular ring a=axa for some x in R, giving the equation a(xa-1)=0. Since a is not a zero divisor, xa=1, showing a is a unit. Here again, 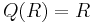 .
.
Applications
In algebraic geometry one considers a sheaf of total quotient rings on a scheme, and this may be used to give one possible definition of a Cartier divisor.
Generalization
If  is a commutative ring and
is a commutative ring and  any multiplicative submagma of
any multiplicative submagma of  with unit, one can construct the
with unit, one can construct the 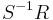 in a similar fashion, where only elements of
in a similar fashion, where only elements of  are possible denominators. If
are possible denominators. If 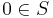 , then
, then 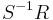 is the trivial ring. For details, see Localization of a ring.
is the trivial ring. For details, see Localization of a ring.
Notes
- ^ Matsumura (1980), p. 12
- ^ Matsumura (1989), p. 21
- ^ If one supposes a is a nonzero zero divisor in R and also a unit in its total ring of quotients Q, then ab=0 for some nonzero b in R and ca=1 for a c in Q, and then 0=c(ab)=(ca)b=b, but b was assumed to be nonzero. This contradiction shows a zero divisor of R cannot be a unit in Q.
References
- Hideyuki Matsumura, Commutative algebra, 1980
- Hideyuki Matsumura, Commutative ring theory, 1989